Rotacional, divergencia y gradiente.
El rotacional.
El
rotacional de una función vectorial es el producto vectorial del operador
Nabla con una función vectorial:
Donde
i,j,k son los vectores unitarios en las direcciones x, y, z. También
se puede expresar en la forma de un determinante:
El rotacional en
un sistema de coordenadas polar cilíndrica, expresado en la forma de
un determinante es:
El rotacional en un sistema de coordenadas polar esférica,
expresado en la forma de undeterminante es:
Divergencia.
La divergencia de un campo vectorial:
en coordenadas
rectangulares se define como el producto escalar del operador
nabla por la función
En coordenadas polar cilíndrica:
y en coordenadas polar esférica:
Gradiente.
El gradiente es una operación
vectorial, que opera sobre una función escalar, para producir un vector cuya
magnitud es la máxima razón de cambio de la función en el punto del gradiente y
que apunta en la dirección de ese máximo. En coordenadas rectangulares el
gradiente de la función f(x,y,z) es:
Si S es una superficie de valor constante, para la función
f(x,y,z), entonces el gradiente sobre la superficie, define un vector que es
normal a la superficie.
Comparado al gradiente en coordenadas
rectangulares:
En coordenadas polar cilíndrica :
y en coordenadas polar esférica :










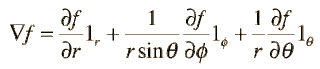


Comentarios
Publicar un comentario